Las ecuaciones lineales son un sistema de ecuaciones de la siguiente forma:
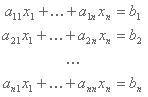
Donde aij y bj son constantes, mientras que xj son variables. Cuando todos los términos bj son iguales a cero, decimos que el sistema es homogéneo, mientras que en cualquier otro caso es no homogéneo.
Estas ecuaciones se pueden representar mediante la matriz aumentada:
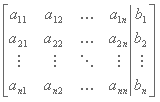
Los dos métodos más comunes para resolver este tipo de sistemas son el método de eliminación gaussiana con sustitución hacia atrás y el método de eliminación Gauss-Jordan.
En el primer método, lo que buscamos es reducir la ecuación a una forma triangular, una vez que hacemos esto, el valor de xn es inmediato y los demás los podemos ir calculando al sustituir los que ya obtuvimos de forma regresiva.
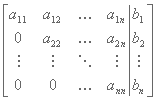
Para el segundo método, reducimos el sistema a una matriz diagonal con lo que podemos encontrar las soluciones directamente:
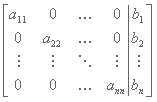
La forma para reducir la matriz a su forma triangular o diagonal es multiplicando un renglón por una constante y sumándoselo a otro. Por ejemplo, al empezar queremos hacer que debajo a11 todos los valores sean cero. Para eliminar el a21 en el segundo renglón, multiplicamos el primero por
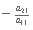 y se lo sumamos al segundo. Podemos obtener los demás ceros de manera similar, utilizando a los demás valores de la diagonal.
y se lo sumamos al segundo. Podemos obtener los demás ceros de manera similar, utilizando a los demás valores de la diagonal.A los valores que tomamos en la matriz para hacer cero a los demás se les conoce como pivotes. Existe el problema de que si el pivote es cero, no podemos eliminar a los demás valores (por la división que efectuamos). En este caso, cambiamos el renglón por otro que no contenga un cero en esa posición.
La complejidad de ambos métodos es O(n3). Con la sustitución hacia atrás se realizan menos operaciones, pero Gauss-Jordan es un poco más sencillo de implementar, además de que podemos cambiar a los valores de b por la matriz identidad para obtener la inversa de la matriz.
El invierno ha llegado, pero en la Universidad Estatal de Ural todavía no se enciende la calefacción. Existe un pequeño problema: la calefacción solo funciona si todas las válvulas están abiertas. La universidad cuenta con varios técnicos, y cada uno es responsable de una o más válvulas. Cuando a un técnico se le da la instrucción de girar las válvulas, visita todas las válvulas que le corresponden y las gira. Esto quiere decir que si una válvula estaba abierta entonces la cierra, y si estaba cerrada la abre. Es bien sabido que un técnico no trabaja en vano, por lo que es imposible reemplazar a un técnico mediante la combinación de otros.
Solución: Podemos resolver este problema mediante las ecuaciones:
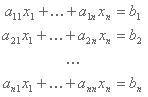
Donde xj representa al j-ésimo técnico y cada renglón representa una válvula. Los coeficientes aij toman los valores de 0 o 1 de acuerdo a si el j-ésimo técnico tiene asignada la i-ésima válvula. Al sumar la cantidad de técnicos que mueven una válvula, nos tiene que dar un número impar para que quede abierta, por lo que la ecuación módulo dos nos queda de la siguiente manera:
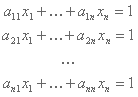 (mod 2)
(mod 2)
Como la cantidad de técnicos es igual a la cantidad de válvulas y ningún técnico es combinación lineal de los demás, siempre va a existir alguna solución.

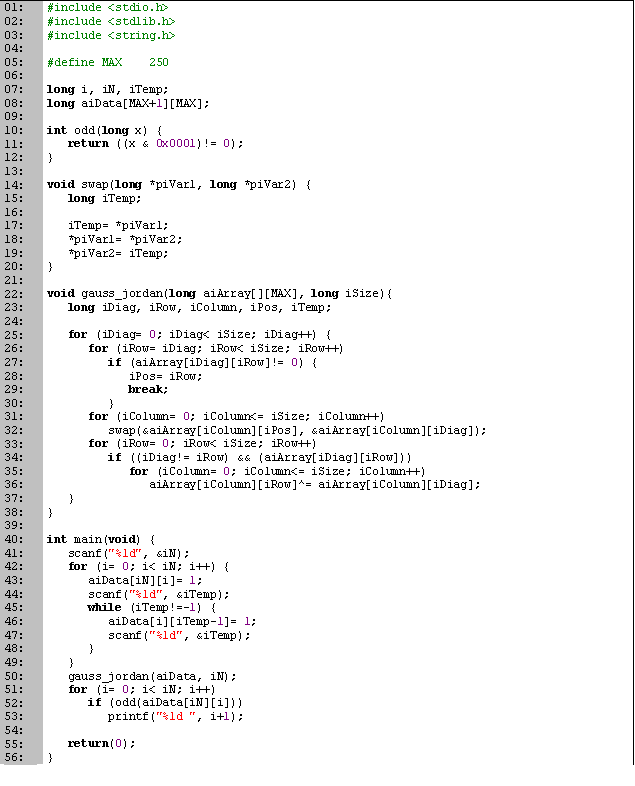
En las primeras tres líneas declaramos las variables que vamos a utilizar. Para los ciclos utilizamos i, para la cantidad de técnicos n, y t como variable temporal. La matriz expandida la guardaremos en el arreglo m.
En seguida tenemos el procedimiento Gauss_Jordan (líneas 5 a 25), que es donde encontramos la solución del sistema. Los enteros i, j y k los utilizamos para los ciclos, t como variable temporal y p para buscar el pivote. Para cada elemento de la diagonal (línea 8), buscamos el primer elemento en la columna que sea distinto de cero (líneas 10 a 15) y una vez que lo que encontramos, intercambiamos renglones (líneas 16 a 19). Para eliminar los demás valores de la diagonal, utilizamos el ciclo de la línea 20. Si encontramos algún valor que sea distinto de cero y no sea el actual (línea 21), eliminamos ese valor (líneas 22 y 23). Para hacerlo, realizamos una OR exclusiva entre los dos renglones. Esto se debe a que los valores de m[i, i] y m[i, j] son uno, por lo que para eliminar el renglón j tendríamos que multiplicar el i por –1 y sumárselo al j. Al sumar los valores se pueden presentar dos casos: si en m[k, i] tenemos un cero entonces el valor en m[k, j] permanece igual, pero si tenemos un 1, entonces pasa de abierto a cerrado o viceversa.
| Entrada: |
4 1 2 -1 2 3 4 -1 2 -1 4 -1 |
| Desarrollo: |
m[] 1000|1 1110|1 0100|1 0101|1 i= 1 1000|1 0110|0 0100|1 0101|1 i= 2 1000|1 0110|0 0010|1 0011|1 i= 3 1000|1 0100|1 0010|1 0001|0 i= 4 1000|1 0100|1 0010|1 0001|0 |
| Salida: | 1 2 3 |
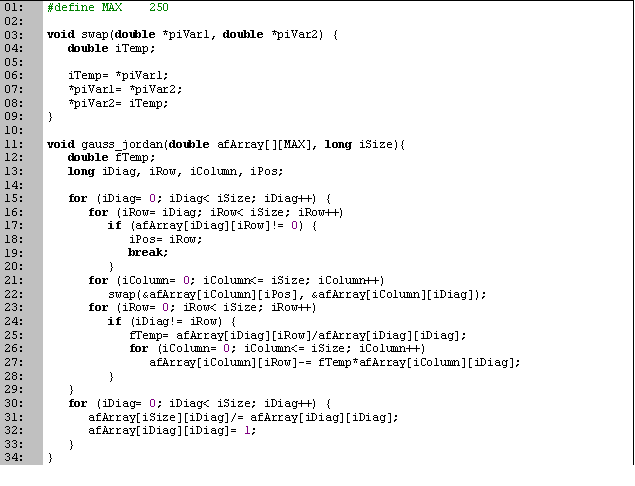
Para utilizar el método en una ecuación donde los valores son reales, podemos modificarlo de la siguiente manera.

Las variables son las mismas que en la implementación anterior, sólo que cambiamos t y m a tipo flotante. Hasta la línea 19 realizamos los mismos pasos, y en el ciclo de la línea 20 en lugar de utilizar la operación XOR, eliminamos sumando el renglón multiplicado por el resultado de
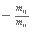 (líneas 23 a 25). Una vez que tenemos diagonalizado, hacemos que los valores de las diagonales sean 1 para encontrar los resultados (líneas 28 a 33).
(líneas 23 a 25). Una vez que tenemos diagonalizado, hacemos que los valores de las diagonales sean 1 para encontrar los resultados (líneas 28 a 33).En este código estamos intercambiando renglones cuando el pivote es cero. Como estamos trabajando con números flotantes, si el pivote está muy cercano a cero, se pueden introducir errores de redondeo. Para evitar esto, podemos buscar el elemento de mayor valor absoluto de la columna en los renglones restantes para después intercambiar columnas. A esto se le conoce como pivoteo parcial. Lo podemos agregar modificando el ciclo de la línea 10 para que buscar el mayor valor absoluto, en lugar del primero que sea distinto de cero.
Otra opción es buscar al mayor elemento sobrante en la matriz (no sólo en la columna), para después intercambiar renglones y columnas de tal manera que este quede como pivote. A esto se le conoce como pivoteo completo (o máximo). Para agregárselo al código, tendríamos que anidar un ciclo en el de la línea 10 (de k = i hasta n) para buscar el mayor elemento, y agregar el intercambio de columnas después.
Un elemento más que sería importante agregar es una comprobación para cuando las soluciones no son únicas. Para hacerlo, sólo debemos revisar si en algún momento no es posible encontrar algún pivote que sea distinto de cero.
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 17-May-2006 | 0.015 | 0.001 | 0.010 | 0.961 | 234 |
| C | 17-May-2006 | 0.001 | 238 | |||
Valladolid:
 Raíces de ecuaciones de una variable (Bisección y Newton)
Raíces de ecuaciones de una variable (Bisección y Newton)
