Dados dos números naturales a y b, denominamos como divisores comunes al conjunto de números que dividen tanto a a como a b. El mayor elemento de este conjunto recibe el nombre de máximo común divisor (mcd). Por ejemplo, los divisores de 63 son {1, 3, 7, 9, 21, 63} y de 105 son {1, 3, 5, 7, 15, 21, 35, 105}, los divisores comunes son la intersección de los conjuntos, con lo que obtenemos {1, 3, 7, 21}. Por lo tanto, el mcd de 63 y 105 es 21. Cuando el máximo común divisor de dos números es uno, se dice que estos números son primos relativos.
Si en lugar de tener los conjuntos de divisores de a y b, utilizamos los de los múltiplos, al realizar la intersección de estos obtenemos el conjunto de los múltiplos comunes. Al menor elemento de este conjunto lo denominamos el mínimo común múltiplo (mcm). Utilizando de nuevo 63 y 105, los múltiplos del primero son {63, 126, 189, ...}, los del segundo {105, 210, 315, ...}, su intersección es {315, 630, 945, ...}, por lo que el mcm de 63 y 105 es 315.
También podemos obtener el mcd y el mcm descomponiendo a a y b en su factorización por primos (tema 4.6). Comparando los dos números, para encontrar el mcd utilizamos el menor exponente de cada primo. Para obtener el mcm, empleamos el mayor exponente de cada primo. Utilizando los mismos números de los ejemplos anteriores, 63 = 20×32×50×71 y 105 = 20×31×51×71, por lo tanto el mcd será 20×31×50×71 = 21 y el mcm 20×32×51×71 = 315.
El problema de este método es que la factorización de un número es un proceso lento. Una forma más eficiente para obtener el mcd es utilizar el Algoritmo de Euclides, el cual utiliza la siguiente fórmula:
mcd(a,b) = mcd(min(a,b), |a-b|)
Que también puede ser expresada como:
mcd(a,b) = mcd(b, a mod b)
Por la forma del algoritmo, su implementación recursiva es casi inmediata aunque una implementación iterativa puede ayudar a obtener un mejor rendimiento. La primera fórmula puede resultar conveniente para números grandes (capítulo 6), aunque generalmente la segunda es mucho más eficiente.
El mínimo común múltiplo lo podemos obtener rápidamente una vez que calculemos el máximo común divisor, ya que lo único que debemos hacer es dividir el primer número por el máximo común divisor para después multiplicar el resultado por el segundo número. Esto es:
mcm(a,b) =
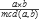
Problema ejemplo
Mínimo Común Múltiplo
Problema
El mínimo común múltiplo (mcm) de un conjunto de enteros positivos es el menor entero positivo que es menor entero positivo que es divisible por todos los números del conjunto. Por ejemplo, el mcm de 5, 7 y 15 es 105.Entrada
La entrada consiste en varios casos. La primera línea de la entrada contiene un único entero que indica la cantidad de casos. Cada caso consiste en una línea de la forma m n1 n2 n3 ... nm, donde m es la cantidad de enteros en el conjunto y n1 ... nm son dichos enteros. Todos los enteros serán positivos y estarán en el rango de un entero de 32 bits.Salida
Para cada caso, la salida consistirá en una línea con el mcm correspondiente. Todos los resultados estarán en el rango de un entero de 32 bits.Solución: Para calcular el mcm (o el mcd) de más de dos números, basta con calcularlo para los primeros dos, después calculamos el mcm entre el resultado y el tercer número, y así sucesivamente con los demás números.
Código

Comenzamos declarando entre las líneas 1 y 2 las variables a utilizar. Para los ciclos emplearemos i y j, c para la cantidad de casos, m para la cantidad de enteros en cada caso, t como variable temporal y n para guardar el resultado. Como los números son enteros positivos de 32 bits, utilizamos variables de tipo cardinal (equivalente a longword).
En la función mcd calculamos el máximo común divisor de los parámetros a y b. La implementación es directa, siguiendo el algoritmo de Euclides. La línea 6 es la fórmula recursiva, mientras que la 7 es el caso base que hace que la recursividad termine.
La siguiente función, mcm, es en la que calculamos el mínimo común múltiplo. En la línea 13 calculamos el mcm empleando el mcd. Para evitar desbordamientos, primero efectuamos la división y después la multiplicación; y para evitar divisiones entre cero, revisamos que ni a ni b sean cero (línea 12).
Entre la línea 16 y 29 tenemos la parte principal del programa. En la línea 17 leemos la cantidad de casos a procesar. Después, en la línea 20 leemos m y n. Continuamos calculado el mcm entre el resultado anterior (que en el inicio es el primer número) y cada nuevo número que leemos (líneas 21 a 25). Terminamos pasando a la siguiente línea en la entrada y escribiendo el resultado en la salida (líneas 26 y 27).Casos ejemplo
| Entrada: | 1 3 5 15 7 |
| Desarrollo: | mcd( 5,15) = mcd(15, 5 mod 15) mcd(15, 5) = mcd( 5, 15 mod 5) mcd( 5, 0) = 5 mcm( 5,15) = (5/5)×15 = 15 mcd(15, 7) = mcd(7, 15 mod 7) mcd( 7, 1) = mcd(1, 7 mod 1) mcd( 1, 0) = 1 mcm(15, 7) = (15/1)×7 = 105 mcm(5,15,7) = 105 |
| Salida: | 105 |
| Entrada: | 1 3 25 58 3 |
| Desarrollo: | mcd(25,58) = mcd(58, 25 mod 58) mcd(58,25) = mcd(25, 58 mod 25) mcd(25, 8) = mcd(8, 25 mod 8) mcd( 8, 1) = mcd(1, 8 mod 1) mcd( 1, 0) = 1 mcm(25,58) = (25/1)×58 = 1450 mcd(1450,3) = mcd(3, 1450 mod 3) mcd( 3, 1) = mcd(1, 3 mod 1) mcd( 1, 0) = 1 mcm(1450,3) = (1450/1)×3 = 4350 mcm(25,58,3) = 4350 |
| Salida: | 4350 |
Información adicional
La complejidad del algoritmo de mcd es de O(lgn), y el peor caso se da cuando tenemos por entrada dos números de Fibonacci consecutivos (sección 5.6). Esto se debe, en parte, a que dos números consecutivos de Fibonacci siempre son primos relativos.
Existe una variación de este algoritmo conocida como algoritmo mcd binario. Este algoritmo tiene la misma complejidad que el que vimos, pero tiene la ventaja de no utilizar módulos por lo que es más eficiente. Aunque fue publicado hace algunas décadas (1961 por Josef Stein), se cree que los chinos ya lo conocían desde el siglo I.
El algoritmo se basa en lo siguiente:
- Si a y b son pares, entonces mcd(a,b) = 2×mcd(
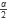 ,
,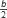 ).
). - Si a y b son impares, entonces mcd(a,b) = mcd(min(a,b), |a-b|).
- Si sólo a es impar, entonces mcd(a,b)= mcd(a,
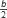 ) (se hace de manera análoga para b impar).
) (se hace de manera análoga para b impar).
Algunas de las desventajas de este método, es que sólo puede ser utilizado para números naturales, y no puede obtenerse una versión extendida del algoritmo (ver siguiente sección).
El algoritmo de Euclides también puede ser utilizado para encontrar la representación de una fracción en forma continua, es decir, una fracción de la forma:
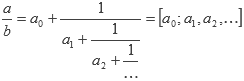
Para hacerlo, tomamos el cociente de
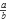 en cada etapa del algoritmo. Por ejemplo, para los números a = 25 y b = 58, tenemos que:
en cada etapa del algoritmo. Por ejemplo, para los números a = 25 y b = 58, tenemos que:mcd(25,58) = mcd(58, 25 mod 58);
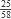 = 0
= 0mcd(58,25) = mcd(25, 58 mod 25);
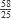 = 2
= 2mcd(25,8) = mcd(8, 25 mod 8);
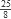 = 3
= 3mcd(8,1) = mcd(1, 8 mod 1);
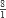 = 8
= 8mcd(1,0) = 1
Por lo que:
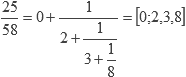
El método también puede ser utilizado cuando a y b son reales, por lo que puede ser empleado para representar números irracionales, aunque la sucesión de cocientes sería infinita.
Código en C

Tiempo de ejecución
| Lenguaje | Fecha | Tiempos [s] | Memoria [Kb] | |||
|---|---|---|---|---|---|---|
| Ejecución | Mejor | Mediana | Peor | |||
| Pascal | 13-Ene-2006 | 0.010 | 0.000 | 0.000 | 0.930 | 308 |
| C | 17-Feb-2006 | 0.010 | 388 | |||
Otros problemas
Valladollid:
Ural:
Saratov:
 Introducción
Introducción
